
Investigation of different target materials of medical linac on photon percentage depth-dose profiles: PHITS Monte Carlo study
Highlight box
Key findings
• Resultant percentage depth-dose (PDD) analysis shows increasing trends for copper with energy, while gold and tungsten maintained consistent edges.
• Copper demonstrates the highest tissue-phantom ratio values, indicating enhanced beam penetration capability.
What is known and what is new?
• Numerous Monte Carlo (MC) tools are frequently employed in linear accelerator (linac) simulations. These commonly used tools include Geant4, MCNP, FLUKA, EGSnrc (BEAMnrc/DOSXYZnrc), and PENELOPE. Nevertheless, in our research, we utilize the general-purpose MC code known as Particle and Heavy Ion Transport code System (PHITS) which can deal with the particle transport of all particles over wide energy ranges which utilize nuclear reaction models and nuclear data libraries. Since PHITS is relatively new, there are limited studies that deal on the investigation of various target materials in the medical linac head.
What is the implication, and what should change now?
• The increasing trends in PDD analysis for copper with energy and its highest tissue-phantom ratio values imply that copper could be a preferred target material in linacs for applications requiring enhanced beam penetration and dose delivery efficiency.
Introduction
Since Wilhelm Röntgen’s discovery of X-rays in 1895, X-ray testing has become a prevalent method for examining the internal structures of objects (1,2). This technique finds extensive applications in various fields, including medicine, industry, security, and scientific research (3). Each of these applications has specific requirements, such as a particular X-ray energy, radiation dose, and imaging time. One of the devices capable of generating X-rays is a medical linear accelerator (linac), utilizing bremsstrahlung radiation (1). A linac uses X-rays or photons produced by accelerating electrons with high voltage and hitting them with a target; in other situations, electron beams themselves are employed. The target is crucial in the production of X-rays as it interacts with electrons. Several factors affect X-ray generation include the atomic number, mass number, and thickness of the target’s component elements (4). Targets with high atomic numbers (high Z), such as tungsten, gold, silver, tantalum (5), and copper (6) are utilized to generate high-energy X-rays.
Presently, with the Monte Carlo (MC) method, it is possible to calculate the radiation distribution resulting from interactions with the surrounding environment and quantify scattered radiation. This approach allows for a straightforward examination of how radiation interacts with the material.
The scarcity of research exploring the properties of photons produced by different targets in the linac head has motivated us to conduct this study, focusing on two main objectives. Firstly, to simulate and investigate the depth dose profiles of photon beams generated by different target materials, namely copper, gold, and tungsten, within a homogeneous water phantom using the Particle and Heavy Ion Transport code System (PHITS) (7,8). Various electron source energies are utilized to investigate their impact of target material on the depth dose profiles. In addition, the simulated photon depth dose profile distributions are compared with an empirical model using the modified build-tail functions (9) and the investigation of the linear energy transfer (LET) at different target materials is carried out.
Methods
PHITS MC Simulation Toolkit
The MC simulations of a medical linac were conducted using the PHITS (7,8). PHITS version 3.27 was used in this study. The PHITS code system is a general-purpose MC PHITS which can estimate the transport of particles through any medium across a broad energy range using various nuclear reaction models and data libraries. The usefulness and accuracy of PHITS has been demonstrated in several research areas, including heavy ion radiotherapy, space radiation dosimetry and accelerator-shielding experiments (10,11). Nearly all radiation in the three-dimensional (3D) geometry of objects can be simulated by PHITS (12). In addition, its memory usage is substantially smaller, irrespective of the phantom’s intricacy and the quantity of threads (13). At lower proton energies, PHITS produced secondary neutrons in a considerably more forwardly oriented way than MCNP6 and TOPAS and for out-of-field organs, PHITS gave similar dose estimates with TOPAS. In terms of MC code efficiency, PHITS was the most effective code for calculating out-of-field neutron dose by almost a factor of ten. Additionally, PHITS was the most accurate in calculating the gamma dose from out-of-field by around two orders of magnitude (14).
Simulation setup
In this study, three target materials in the linac head, namely, tungsten (W), copper (Cu) and gold (Au) of uniform thickness 0.2 cm were used. Each simulation includes primary and secondary collimators, 1.5 cm thick Cu flattening filter, and jaw. The primary and secondary collimator components were made of tungsten, nickel (Ni), and iron (Fe). The beam field size was set to 10×10 cm2 and the source-to-surface distance was kept at 100 cm. In the simulation setup, a homogeneous water phantom measuring 30×30×30 cm3 was utilized. A monoenergetic axial electron beam source consisting of 5×107 particles with beam radius of 0.10 cm was employed, with varying initial beam energies of 10, 15, and 20 MeV. The voxel size was 0.3×0.3 cm2. The percentage depth-dose (PDD) profile curves were obtained along the central axis. The default electron cutoff energy parameters for electrons and photons in PHITS were set to 0.1 and 0.01 MeV, respectively. Statistical uncertainty obtained in PHITS simulation was less than 0.1%. Other physics options (e.g., variance reduction, event generator, etc.) were kept at default settings. The linac head model used in the simulation is depicted in Figure 1.
PDD distribution
The PDD profile curves for photon beams in this study were modeled using the modified buildup and tail functions (7). The buildup function is represented by a quadratic form of , where d is the depth in water in centimeters (cm), and is a unitless beam hardening factor. On the other hand, the tail function is expressed as , where d is the depth in water in cm, and is the linear attenuation coefficient factor in cm−1, responsible for adjusting the slope of the tail. The tail function consists of an exponential function with the main parameters of d and .
The overall empirical function for the PDD, denoted as PDDb-t (the abbreviation of PDDbuild-tail), is the combination of these two functions (7):
By varying the parameters n and to get the best fitting, the buildup-tail function in this study was used to represent the PDD of the various photon energies.
LET
When a particle passes through tissue, it deposits energy that was described by LET. In radiation therapy, the depth-dose profile and LET are tightly related, with increased LET found in the vicinity of the Bragg peak (15). This minimizes damage to the surrounding healthy tissue by concentrating all of the energy at the site of the tumor. Visualization of the LET in this study was obtained from the simulation result from PHITS.
Beam quality index, tissue-phantom ratio in water at depths of 20 and 10 cm (TPR20,10)
To validate the beam quality, the quality index through the TPR20,10 for a 10×10 cm2 treatment field size was obtained and compared with the empirical model. This TPR20,10 was calculated using the empirical formula (16) given by
where, represents the PDD at a depth of 20 cm, while PDD10 denotes the PDD at a depth of 10 cm. Ethical approval and informed consent were not required for this study because it did not involve human or animal participants, nor did it entail the use of personal data.
Results
Figure 2 illustrates the PDD profile curves acquired using PHITS for copper, gold, and tungsten materials at varying energies of 10, 15, and 20 MeV. Large deviations in the photon’s dose build-up region are observed than in the tail regions due to free electron’s interaction. The visual representations of the PHITS-simulated PDDs and their corresponding models (from empirical function) for copper, gold, and tungsten at 20 MeV energy are shown in Figure 3. The ideal values of the parameters n and μ, which produce the best fitting with empirical formula, are listed in Table 1. Table 2 provides information on the percentage difference in TPR20,10 values among various target materials. Furthermore, Figures 4-6 display the LET values for copper, gold, and tungsten at energy levels of 10, 15, and 20 MeV, respectively.

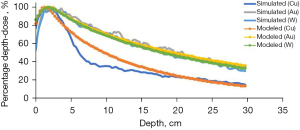
Table 1
| Materials | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| 10 Mev | 15 MeV | 20 MeV | ||||||
| Copper | 0.900 | 0.099 | 0.900 | 0.070 | 2.500 | 0.070 | ||
| Gold | 2.500 | 0.035 | 2.500 | 0.033 | 5.000 | 0.033 | ||
| Tungsten | 5.000 | 0.042 | 5.000 | 0.036 | 5.000 | 0.0336 | ||
Table 2
| Materials | TPR20,10 (difference) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 MeV | 15 MeV | 20 MeV | |||||||||
| MC simulated | Calculated | Difference | MC simulated | Calculated | Difference | MC simulated | Calculated | Difference | |||
| Copper | 0.9120 | 0.5072 | 0.4048 | 0.7372 | 0.5682 | 0.1690 | 0.7697 | 0.5682 | 0.2015 | ||
| Gold | 0.7487 | 0.7977 | 0.0489 | 0.7381 | 0.8182 | 0.0801 | 0.2015 | 0.8128 | 0.0054 | ||
| Tungsten | 0.9305 | 0.7485 | 0.1820 | 0.7049 | 0.7925 | 0.0877 | 0.8182 | 0.7537 | 0.0388 | ||
TPR20,10, tissue-phantom ratio at 20 and 10 cm depths; MC, Monte Carlo.



Discussion
The PHITS-simulated PDD profile curves when copper, gold, and tungsten as target materials of uniform thickness in the linac head are irradiated with varying energies of 10, 15, and 20 MeV are shown in Figure 2. As observed, as the energy increases, the PDD profile curve also increases and the maximum dose depositions per depth show an increasing trend as the target material’s atomic number considered increases. This is evident for the copper target. In addition, for the gold and tungsten target materials, despite the increase in energy, the edge of their PDD profile curves remain unchanged. Copper, however, shows a distinct dose profile due to its lower density compared to gold and tungsten.
Graphical depictions of PHITS-simulated and modelled PDDs for copper, gold, and tungsten at different energies are presented in Figure 3. The model is obtained by implementing empirical function presented in Eq. [1]. Table 1 lists the optimal values of parameters n and μ, which result in the best fit. Analyzing the graph and the values of n and μ, it becomes evident that copper diverges significantly in its hardening factor (n) and linear attenuation coefficient (μ) compared to gold and tungsten. This divergence might be attributed to the differences in atomic number (Z) and density since copper as compared with gold and tungsten, has lower density and Z value. In addition, it is observed that as energy increases, the linear attenuation coefficient decreases. Target materials with higher photon energy allow for a greater number of photons to pass through than lower photon energy ones. They attenuate low-energy X-rays more severely than high-energy ones. Because they are less likely to interact with matter, higher energy photons pass through tissue more readily than lower energy photons. Likewise, as the beam attenuates, the remaining energy decreases as shown in Figure 3.
Table 2 displays the difference in TPR20,10 among different target materials. At an energy of 10 MeV, the MC simulated TPR20,10 for copper is 0.9120, contrasting with the calculated value of 0.5072, resulting in a deviation of 0.4048. Similarly, for gold, the MC simulated TPR20,10 stands at 0.7487, while the calculated value is 0.7977, yielding a deviation of 0.0489. Meanwhile, tungsten exhibits an MC simulated TPR20,10 of 0.9305, with a calculated value of 0.7485, resulting in a deviation of 0.1820. At 15 MeV, the copper material’s MC simulated TPR20,10 is 0.7372, whereas the calculated value is 0.5682, leading to a deviation of 0.1690. As for gold, its MC simulated TPR20,10 is 0.7381, and the calculated value is 0.8182, with a deviation of 0.0801. Similarly, tungsten demonstrates an MC simulated TPR20,10 of 0.7049, while the calculated value is 0.7925, resulting in a deviation of 0.0877. Lastly, at 20 MeV, the MC simulated TPR20,10 for copper is 0.7697, whereas the calculated value is 0.5682, yielding a deviation of 0.2015. Gold’s MC simulated TPR20,10 is 0.8128, with a minimal deviation of 0.0054, as the calculated value is found to be 0.8182. For tungsten, the MC simulated TPR20,10 stands at 0.7537, while the calculated value is 0.7925, resulting in a deviation of 0.0388. This indicates that for the three energy levels tested, copper exhibits the highest TPR20,10 value. A higher TPR20,10 value corresponds to increased beam penetration (6). This observation is further corroborated by the LET results at different energies presented in Figures 4-6.
Derived from the acquired LET data in PHITS, Figure 4 presents the LET values for copper, gold, and tungsten at an energy level of 10 MeV. It is evident that among the three of mentioned materials, copper exhibits the greatest energy transfer. This observation remains consistent as energy levels escalate to 15 and 20 MeV, as shown in Figures 5,6, respectively. Additionally, there is a clear trend of increasing LET with higher energy levels.
Conclusions
In conclusion, the PDD curves for copper, gold, and tungsten materials at different initial energies using PHITS simulation are examined. As the incident energy increases, the maximum dose deposition of the PDD profile curves also increases for copper, while gold and tungsten exhibited consistent edges in their PDD profiles despite energy variations. Additionally, the beam quality index through the TPR20,10 values for the three materials at 10, 15, and 20 MeV energies are investigated. Copper consistently demonstrates the highest TPR20,10 value, indicating superior beam penetration. The LET results of the various target materials at different incident energies are examined with copper exhibiting the highest LET at all energy levels. Comparison of the simulated PDDs with the empirical model using the modified buildup-tail functions shows virtually how well these values coincide. Overall, the findings provide valuable insights into the behavior of different target materials under varying energy conditions, facilitating improved understanding and potential applications in treatment planning systems in radiation therapy.
Acknowledgments
The authors acknowledge the support extended by Dr. Hiroshi Takemiya, Director of the Center for Computational Science & e-Systems at the Japan Atomic Energy Agency (JAEA) for the use of JAEA Computer Programs particularly the Particle and Heavy Ion Transport code System (PHITS). We also acknowledge the DOST Learning Resource Center for letting us use the computer resources for simulation.
Funding: None.
Footnote
Data Sharing Statement: Available at https://tro.amegroups.com/article/view/10.21037/tro-23-34/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://tro.amegroups.com/article/view/10.21037/tro-23-34/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. Ethical approval and informed consent were not required for this study because it did not involve human or animal participants, nor did it entail the use of personal data.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Mery D. X-ray testing: The state of the art. The e-Journal of Nondestructive Testing 2013;18:01.
- Buaphad P, Kim Y, Song K, et al. X-ray dose rate estimation model for an electron linac with thick tungsten target. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2021;498:61-7. [Crossref]
- Antolak AJ. Overview of accelerator applications for security and defense. Reviews of Accelerator Science and Technology 2015;8:27-36. [Crossref]
- Han DH, Jung KH, Kim JO, et al. Evaluation by thickness of a linear accelerator target at 6-20 MeV electron beam in MCNP6. Nuclear Engineering and Technology 2023;55:1994-8. [Crossref]
- Bilalodin B, Haryadi A, Sardjono Y, et al. Investigation on electron contamination of LINAC at different operating voltages using particle heavy ion transport code system (PHITS). Jurnal ilmiah pendidikan fisika Al-Biruni 2022;11:103-11.
- Tuğrul T. Effect of different target materials of LINAC head on photon spectrum. Journal of Radiation Research and Applied Sciences. 2021;14:204-9. [Crossref]
- Li XJ, Ye YC, Zhang YS, et al. Empirical modeling of the percent depth dose for megavoltage photon beams. PLoS One 2022;17:e0261042. [Crossref] [PubMed]
- Sato T, Niita K, Matsuda N, et al. Overview of particle and heavy ion transport code system PHITS. In: SNA + MC 2013 - Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo. EDP Sciences; 2014:06018.
- Sato T, Iwamoto Y, Hashimoto S, et al. Features of particle and heavy ion transport code system (PHITS) version 3.02. Journal of Nuclear Science and Technology 2018;55:684-90. [Crossref]
- Puchalska M, Sihver L. PHITS simulations of absorbed dose out-of-field and neutron energy spectra for ELEKTA SL25 medical linear accelerator. Phys Med Biol 2015;60:N261-70.
- Iwamoto Y, Hashimoto S, Sato T, et al. Benchmark study of particle and heavy-ion transport code system using shielding integral benchmark archive and database for accelerator-shielding experiments. Journal of Nuclear Science and Technology 2022;59:665-75. [Crossref]
- Niita K, Sato T, Iwase H, et al. PHITS—a particle and heavy ion transport code system. Radiation Measurements 2006;41:1080-90. [Crossref]
- Han MC, Yeom YS, Lee HS, et al. Multi-threading performance of Geant4, MCNP6, and PHITS Monte Carlo codes for tetrahedral-mesh geometry. Phys Med Biol 2018;63:09NT02. [Crossref] [PubMed]
- Griffin KT, Yeom YS, Mille MM, et al. Comparison of out-of-field normal tissue dose estimates for pencil beam scanning proton therapy: MCNP6, PHITS, and TOPAS. Biomed Phys Eng Express 2022; [PubMed]
- Kraft G, KrÄMer M. Linear energy transfer and track structure. In: Advances in Radiation Biology. Elsevier; 1993;17:1-52.
- Followill DS, Tailor RC, Tello VM, et al. An empirical relationship for determining photon beam quality in TG-21 from a ratio of percent depth doses. Med Phys 1998;25:1202-5. [Crossref] [PubMed]
Cite this article as: Dalumpines CG, Peñonal GF, Aringa H, Convicto V. Investigation of different target materials of medical linac on photon percentage depth-dose profiles: PHITS Monte Carlo study. Ther Radiol Oncol 2024;8:6.



